Performance
-
Paper #191: Occam’s Razor for Distributed Protocols
We have been doing a Zoom distributed systems paper reading group for 5 years and have covered around 190 papers. This semester, we should reach the milestone of 200 papers. Over the years, my commitment to the group has varied — at some point, I was writing paper reviews, and more recently, I’ve had less…
-
Pile of Eternal Rejections: The Cost of Garbage Collection for State Machine Replication
I have a “pile” of papers that continuously get rejected from any conference. All these papers, according to the reviews, “lack novelty,” and therefore are deemed “not interesting” by the reviewing experts. There are some things in common in these papers — they are either observational or rely on old and proven techniques to solve a problem or improve a system/algorithm. Jokingly, I call this set of papers the “pile of…
-
Reading Group 151. Towards Modern Development of Cloud ApplicationsReading Group 151.
We kicked off the winter term set of papers in the reading group with the “Towards Modern Development of Cloud Applications” HotOS’23 paper. The paper proposes a different approach to designing distributed applications by replacing the microservice architecture style with something more fluid. The paper argues that splitting applications into microservices from the get-go can…
-
Reading Group. Chardonnay: Fast and General Datacenter Transactions for On-Disk Databases
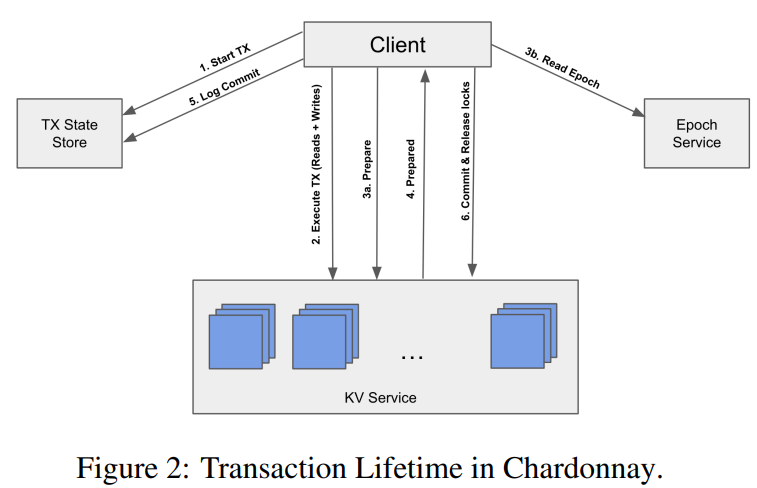
Last week, we looked at the “Chardonnay: Fast and General Datacenter Transactions for On-Disk Databases” OSDI’23 paper by Tamer Eldeeb, Xincheng Xie, Philip A. Bernstein, Asaf Cidon, Junfeng Yang. The paper presents a transactional database built on the assumption of having a very fast two-phase commit protocol. Coordination, like a two-phase commit (2PC), usually has…
-
Cloudy Forecast: How Predictable is Communication Latency in the Cloud?
Many, if not all, practical distributed systems rely on partial synchrony in one way or another, be it a failure detection, a lease mechanism, or some optimization that takes advantage of synchrony to avoid doing a bunch of extra work. These partial synchrony approaches need to know some crucial parameters about their world to estimate…
-
Reading Group. Rabia: Simplifying State-Machine Replication Through Randomization
We covered yet another state machine replication (SMR) paper in our reading group: “Rabia: Simplifying State-Machine Replication Through Randomization” by Haochen Pan, Jesse Tuglu, Neo Zhou, Tianshu Wang, Yicheng Shen, Xiong Zheng, Joseph Tassarotti, Lewis Tseng, Roberto Palmieri. This paper appeared at SOSP’21. A traditional SMR approach, based on Raft or Multi-Paxos protocols, involves a…
-
Reading Group. Exploiting Nil-Externality for Fast Replicated Storage
85th DistSys reading group meeting discussed “Exploiting Nil-Externality for Fast Replicated Storage” SOSP’21 paper by Aishwarya Ganesan, Ramnatthan Alagappan, Andrea C. Arpaci-Dusseau, and Remzi H. Arpaci-Dusseau. The paper uses an old trick of delaying the execution of some operations to improve the throughput while maintaining strong consistency. Consistency is an externally-observable property, and simple strategies,…
-
Reading Group Special Session: Fast General Purpose Transactions in Apache Cassandra
Modern distributed databases employ leader-based consensus protocols to achieve consistency, entailing certain trade-offs: typically either a scalability bottleneck or weak isolation. Leaderless protocols have been proposed to address these and other shortcomings of leader-based techniques, but these have not yet materialized into production systems. This paper outlines compromises entailed by existing leaderless protocols versus leader-based…
-
Reading Group. Characterizing and Optimizing Remote Persistent Memory with RDMA and NVM
We have looked at the “Characterizing and Optimizing Remote Persistent Memory with RDMA and NVM” ATC’21 paper. This paper investigates a combination of two promising technologies: Remote Direct Memory Access (RDMA) and Non-Volatile Memory (NVM). We have discussed both of these in our reading group before. RDMA allows efficient access to the remote server’s memory,…
-
Reading Group. Meerkat: Multicore-Scalable Replicated Transactions Following the Zero-Coordination Principle
Our 72nd paper was on avoiding coordination as much as possible. We looked at the “Meerkat: Multicore-Scalable Replicated Transactions Following the Zero-Coordination Principle” EuroSys’20 paper by Adriana Szekeres, Michael Whittaker, Jialin Li, Naveen Kr. Sharma, Arvind Krishnamurthy, Dan R. K. Ports, Irene Zhang. As the name suggests, this paper discusses coordination-free distributed transaction execution. In…
Search
Recent Posts
- Paper #191: Occam’s Razor for Distributed Protocols
- Spring 2025 Reading List (Papers ##191-200)
- Fall 2024 Reading Group Papers (Papers ##181-190)
- Pile of Eternal Rejections: Revisiting Mencius SMR
- System’s Guy Teaching Game Development…
Categories
- One Page Summary (10)
- Other Thoughts (10)
- Paper Review and Summary (14)
- Pile of Eternal Rejections (2)
- Playing Around (14)
- Reading Group (100)
- RG Special Session (4)
- Teaching (2)