paxos
-
Pile of Eternal Rejections: The Cost of Garbage Collection for State Machine Replication
I have a “pile” of papers that continuously get rejected from any conference. All these papers, according to the reviews, “lack novelty,” and therefore are deemed “not interesting” by the reviewing experts. There are some things in common in these papers — they are either observational or rely on old and proven techniques to solve a problem or improve a system/algorithm. Jokingly, I call this set of papers the “pile of…
-
Reading Group. Amazon DynamoDB: A Scalable, Predictably Performant, and Fully Managed NoSQL Database Service
In the 120th DistSys meeting, we talked about “Amazon DynamoDB: A Scalable, Predictably Performant, and Fully Managed NoSQL Database Service” ATC’22 paper by Mostafa Elhemali, Niall Gallagher, Nicholas Gordon, Joseph Idziorek, Richard Krog, Colin Lazier, Erben Mo, Akhilesh Mritunjai, Somu Perianayagam, Tim Rath, Swami Sivasubramanian, James Christopher Sorenson III, Sroaj Sosothikul, Doug Terry, Akshat Vig.…
-
Reading Group. Rabia: Simplifying State-Machine Replication Through Randomization
We covered yet another state machine replication (SMR) paper in our reading group: “Rabia: Simplifying State-Machine Replication Through Randomization” by Haochen Pan, Jesse Tuglu, Neo Zhou, Tianshu Wang, Yicheng Shen, Xiong Zheng, Joseph Tassarotti, Lewis Tseng, Roberto Palmieri. This paper appeared at SOSP’21. A traditional SMR approach, based on Raft or Multi-Paxos protocols, involves a…
-
Reading Group. Exploiting Nil-Externality for Fast Replicated Storage
85th DistSys reading group meeting discussed “Exploiting Nil-Externality for Fast Replicated Storage” SOSP’21 paper by Aishwarya Ganesan, Ramnatthan Alagappan, Andrea C. Arpaci-Dusseau, and Remzi H. Arpaci-Dusseau. The paper uses an old trick of delaying the execution of some operations to improve the throughput while maintaining strong consistency. Consistency is an externally-observable property, and simple strategies,…
-
Scalable but Wasteful or Why Fast Replication Protocols are Actually Slow
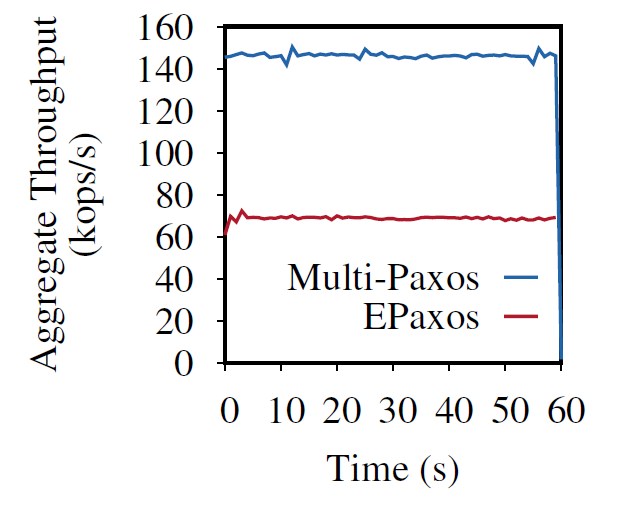
In the last decade or so, quite a few new state machine replication protocols emerged in the literature and the internet. I am “guilty” of this myself, with the PigPaxos appearing in this year’s SIGMOD and the PQR paper at HotStorage’19. There are better-known examples as well — EPaxos inspired a lot of development in…
-
Reading Group. XFT: Practical Fault Tolerance beyond Crashes
In the 57th reading group meeting, we continued looking at byzantine fault tolerance. In particular, we looked at “XFT: Practical Fault Tolerance beyond Crashes” OSDI’16 paper. Today’s summary & discussion will be short, as I am doing it way past my regular time. The paper talks about a fault tolerance model that is stronger than…
-
Reading Group. Protocol-Aware Recovery for Consensus-Based Storage
Our last reading group meeting was about storage faults in state machine replications. We looked at the “Protocol-Aware Recovery for Consensus-Based Storage” paper from FAST’18. The paper explores an interesting omission in most of the state machine replication (SMR) protocols. These protocols, such as (multi)-Paxos and Raft, are specified with the assumption of having a…
-
Reading Group. Paxos vs Raft: Have we reached consensus on distributed consensus?
In our 54th reading group meeting, we were looking for an answer to an important question in the distributed systems community: “What about Raft?” We looked at the “Paxos vs Raft: Have we reached consensus on distributed consensus?” paper to try to find the answer. As always, we had an excellent presentation, this time by…
-
Reading Group. Microsecond Consensus for Microsecond Applications
Our 43rd reading group paper was about an extremely low-latency consensus using RDMA: “Microsecond Consensus for Microsecond Applications.” The motivation is pretty compelling — if you have a fast application, then you need fast replication to make your app reliable without holding it back. How fast are we talking here? Authors go for ~1 microsecond…
-
One Page Summary. Gryff: Unifying Consensus and Shared Registers
This paper by Matthew Burke, Audrey Cheng, and Wyatt Lloyd appeared in NSDI 2020 and explores an interesting idea of a hybrid replication protocol. The premise is very simple – we can take one protocol that solves a part of the problem well, and marry it with another protocol that excels at the second half…
Search
Recent Posts
- Fall 2024 Reading Group Papers (Papers ##181-190)
- Pile of Eternal Rejections: Revisiting Mencius SMR
- System’s Guy Teaching Game Development…
- Summer 2024 Reading Group Papers (Papers ##171-180)
- Pile of Eternal Rejections: The Cost of Garbage Collection for State Machine Replication
Categories
- One Page Summary (10)
- Other Thoughts (10)
- Paper Review and Summary (14)
- Pile of Eternal Rejections (2)
- Playing Around (14)
- Reading Group (98)
- RG Special Session (4)
- Teaching (2)