Aleksey Charapko

Playing Around

  • Cloudy Forecast: How Predictable is Communication Latency in the Cloud?

    ,

    Aleksey Charapko

    ·

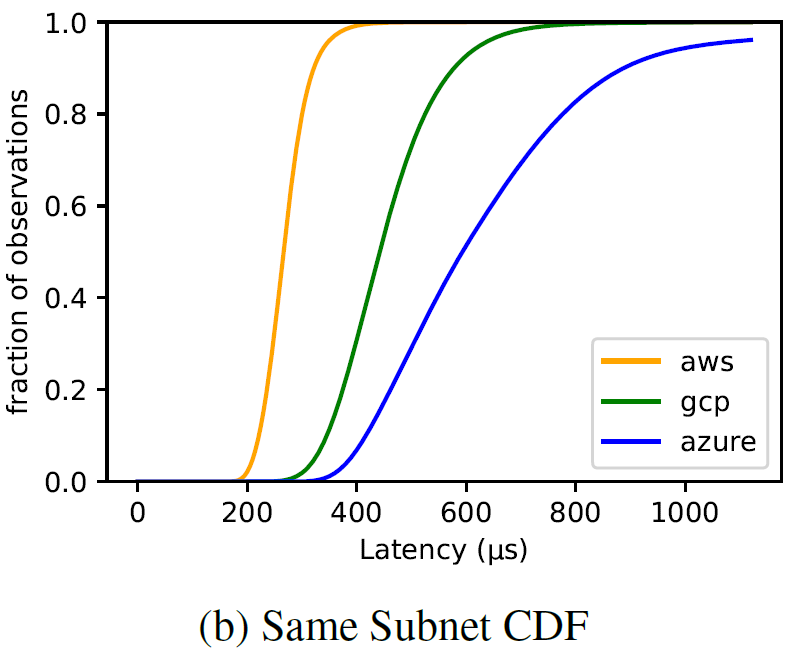
    Many, if not all, practical distributed systems rely on partial synchrony in one way or another, be it a failure detection, a lease mechanism, or some optimization that takes advantage of synchrony to avoid doing a bunch of extra work. These partial synchrony approaches need to know some crucial parameters about their world to estimate…

    Read More

  • PigPaxos: continue devouring communication bottlenecks in distributed consensus.

    Aleksey Charapko

    ·

    This is a short follow-up to Murat’s PigPaxos post. I strongly recommend reading it first as it provides full context for what is to follow. And yes, it also includes the explanation of what pigs have to do with Paxos. Short Recap of PigPaxos. In our recent SIGMOD paper we looked at the bottleneck of…

    Read More

  • Keep The Data Where You Use It

    Aleksey Charapko

    ·

    Placeholder Icon

    As trivial as it sounds, but keeping the data close to where it is consumed can drastically improve the performance of the large globe-spanning cloud applications, such as social networks, ecommerce and IoT. These applications rely on some database systems to make sure that all the data can be accessed quickly. The de facto method…

    Read More

  • Modeling Paxos Performance in Wide Area – Part 3

    Aleksey Charapko

    ·

    Placeholder Icon

    Earlier I looked at modeling paxos performance in local networks, however nowadays people (companies) use paxos and its flavors in the wide area as well. Take Google Spanner and CockroachDB as an example. I was naturally curious to expand my performance model into wide area networks as well. Since our lab worked on WAN coordination…

    Read More

  • Modeling Paxos Performance – Part 2

    Aleksey Charapko

    ·

    Placeholder Icon

    In the previous posts I started to explore node-scalability of paxos-style protocols. In this post I will look at processing overheads that I estimate with the help of a queue or a processing pipeline. I show how these overheads cap the performance and affect the latency at different cluster loads. I look at the scalability for…

    Read More

  • Paxos Performance Modeling – Part 1.5

    Aleksey Charapko

    ·

    Placeholder Icon

    This post is a quick update/conclusion to the part 1. So, does the network variations make any impact at all? In the earlier simulation I showed some small performance degradation going from 3 to 5 nodes. The reality is that for paxos, network behavior makes very little difference on scalability, and in some cases no difference at…

    Read More

  • Do not Blame (only) Network for Your Paxos Scalability Issues. (PPM Part 1)

    Aleksey Charapko

    ·

    Placeholder Icon

    In the past few months our lab has been doing a lot of work with different flavors of paxos consensus algorithm. Paxos and its numerous flavors are widely used in today’s cloud infrastructure. Distributed systems rely on it for many different tasks to ensure safe operation. For instance, coordination services use some consensus protocol flavor…

    Read More

  • Trace Synchronization with HLC

    Aleksey Charapko

    ·

    Placeholder Icon

    Event logging or tracing is one of the most common techniques for collecting data about the software execution. For simple application running on the same machine, a trace of events timestamped with the machine’s hardware clock is typically sufficient. When the system grows and becomes distributed over multiple nodes, each node is going to produce…

    Read More

  • Sonification of Distributed Systems with RQL

    Aleksey Charapko

    ·

    Placeholder Icon

    In the past, I have discussed sonification as a mean of representing monitoring data. Aside from some silly and toy examples, sonifications can be used for serious applications. In many monitoring cases, the presence of some phenomena is more important than the details about it. In such situations, simple sonification is a perfect way to…

    Read More

  • The First Datastore-driven Vehicle

    Aleksey Charapko

    ·

    Placeholder Icon

    It is not a secret that procrastination is the favorite activity of most PhD students. I have been procrastinating today, even though my advisor probably wants me to keep writing.  In the midst of my procrastination, I thought: “Why are there self-driving vehicles, but no database-driven vehicles?” As absurd as it sounds, I gave it…

    Read More

Search

Recent Posts

Categories