Aleksey Charapko
-
Murat and Aleksey Read Papers: “Cloudspecs: Cloud Hardware Evolution Through the Looking Glass”
The “Cloudspecs: Cloud Hardware Evolution Through the Looking Glass” CIDR paper by Till Steinert, Maximilian Kuschewski, and Viktor Leis was the first paper I and Murat read this year. It was a short, but interesting read. Below is our reading video and my one-paragraph summary. The paper discusses the evolution of AWS cloud (virtual) hardware…
-
Murat and Aleksey Read Papers: “Rethinking the Cost of Distributed Caches for Datacenter Services”
Murat and Aleksey read “Rethinking the Cost of Distributed Caches for Datacenter Services.“ This paper argues that distributed caches can save money by reducing CPU costs despite using substantially more of the costly DRAM. The authors claim up to 4X savings in synthetic and open-source workloads. The paper also calls for richer caching semantics to…
-
On Metastable Failures and Interactions Between Systems
I’ve written about metastable failures before. The topic has been picked up by a few different teams since the, all analyzing metastable failures more, while I apparently has been slacking off… Anyway, Metastable failures are self-sustaining performance failures that arise in systems due to a positive feedback loop triggered by an initial problem. This positive…
-
Murat and Aleksey Read Papers: “Barbarians at the Gate: How AI is Upending Systems Research”
The “Barbarians at the Gate: How AI is Upending Systems Research” paper by Audrey Cheng, Shu Liu, Melissa Pan, Zhifei Li, Bowen Wang, Alexander Krentsel, Tian Xia, Mert Cemri, Jongseok Park, Shuo Yang, Jeff Chen, Lakshya Agrawal, Aditya Desai, Jiarong Xing, Koushik Sen, Matei Zaharia, Ion Stoica from Berkeley has recently made a splash in…
-
Academic Chat with Murat and Aleksey: 5 Cs of the Invisible Curriculum.
Instead of reading papers, last night, Murat and I engaged in an interesting discussion on skills, traits, and qualities needed for a PhD. This discussion came as a follow-up to Murat’s recent blog on “The Invisible Curriculum of Research.” In his blog, Murat discusses “Curiosity, Clarity, Craft, Community, and Courage” as skills/qualities of a good…
-
HoliPaxos: Towards More Predictable Performance in State Machine Replication
I will be presenting our new paper, “HoliPaxos: Towards More Predictable Performance in State Machine Replication,” at the VLDB’25. Feel free to ping me if you are there and want to chat! This paper explores several orthogonal optimizations to the classical MultiPaxos state machine replication protocol to improve its performance stability in the presence of…
-
Fall 2025 Reading List (##201-210)
Here is a list for the Fall 2025 semester. Please join the reading group here: https://discord.gg/VS7J4PAU58. We meet on Thursdays. The schedule is also available on our calendar.
-
Paper #196. The Sunk Carbon Fallacy: Rethinking Carbon Footprint Metrics for Effective Carbon-Aware Scheduling
The last paper we covered in the Distributed Systems Reading group discussed CPUs, data centers, scheduling, and carbon emissions—we read “The Sunk Carbon Fallacy: Rethinking Carbon Footprint Metrics for Effective Carbon-Aware Scheduling.” Below is my improvised presentation of this paper for the reading group. This paper was an educational read for me, as I learned…
-
Paper #193. Databases in the Era of Memory-Centric Computing
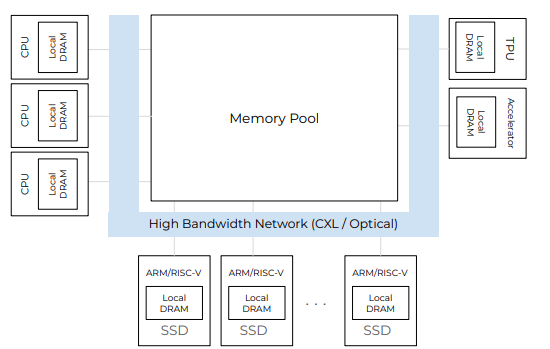
Last week, we read “Databases in the Era of Memory-Centric Computing” CIDR’25 paper in our reading group. This paper argues that the rising cost of main memory and lagging improvement in memory bandwidth do not bode well for traditional computing architectures centered around computing devices (i.e., CPUs). As CPUs get more cores, the memory bandwidth…
-
Paper #192. OLTP Through the Looking Glass 16 Years Later: Communication is the New Bottleneck
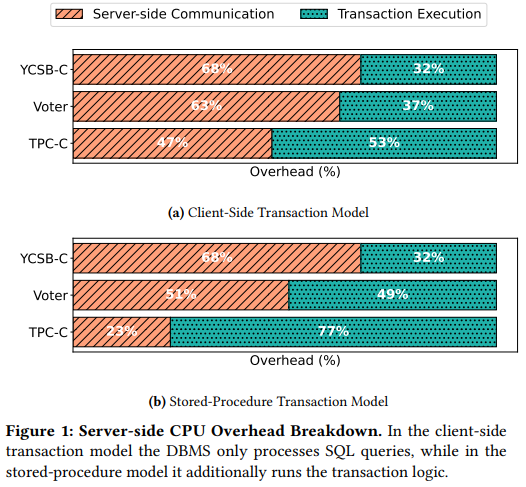
Last week we read “OLTP Through the Looking Glass 16 Years Later: Communication is the New Bottleneck” CIDR’25 paper by Xinjing Zhou, Viktor Leis, Xiangyao Yu, Michael Stonebraker. This paper revisits the original “OLTP Through the Looking Glass, and What We Found There” paper and examines the bottlenecks in modern OLTP databases. The new paper…
Search
Recent Posts
- Murat and Aleksey Read Papers: “Cloudspecs: Cloud Hardware Evolution Through the Looking Glass”
- Murat and Aleksey Read Papers: “Rethinking the Cost of Distributed Caches for Datacenter Services”
- On Metastable Failures and Interactions Between Systems
- Murat and Aleksey Read Papers: “Barbarians at the Gate: How AI is Upending Systems Research”
- Academic Chat with Murat and Aleksey: 5 Cs of the Invisible Curriculum.
Categories
- One Page Summary (11)
- Other Thoughts (15)
- Paper Review and Summary (16)
- Pile of Eternal Rejections (2)
- Playing Around (14)
- Reading Group (104)
- RG Special Session (4)
- Teaching (2)