-
Spring 2024 Reading Group Papers (##161-170)
Below is the reading group schedule for the upcoming winter term. The schedule is also available in our Google Calendar. Are you interested in joining the reading group? It is simple, join our Slack to get all the reading group updates and invites.
-
Reading Group #153. Deep Note: Can Acoustic Interference Damage the Availability of Hard Disk Storage in Underwater Data Centers?
For the 153rd reading group paper, we read something very different this time: “Deep Note: Can Acoustic Interference Damage the Availability of Hard Disk Storage in Underwater Data Centers?” This HotStorage short paper explores the possibility of using soundwaves to attack underwater data centers. In particular, the paper shows how magnetic disks can be disrupted…
-
Reading Group #152. Blueprint: A Toolchain for Highly-Reconfigurable Microservice Applications
The 152nd reading group meeting continued the microservices discussion started in the 151st paper. We read the “Blueprint: A Toolchain for Highly-Reconfigurable Microservice Applications” SOSP’23 paper by Vaastav Anand, Deepak Garg, Antoine Kaufmann, and Jonathan Mace. The premise of the Blueprint is the separation of the app’s logic and most of the infrastructure/ops concerns. This…
-
Reading Group 151. Towards Modern Development of Cloud ApplicationsReading Group 151.
We kicked off the winter term set of papers in the reading group with the “Towards Modern Development of Cloud Applications” HotOS’23 paper. The paper proposes a different approach to designing distributed applications by replacing the microservice architecture style with something more fluid. The paper argues that splitting applications into microservices from the get-go can…
-
Reading Group #150. Model Checking Guided Testing for Distributed Systems.
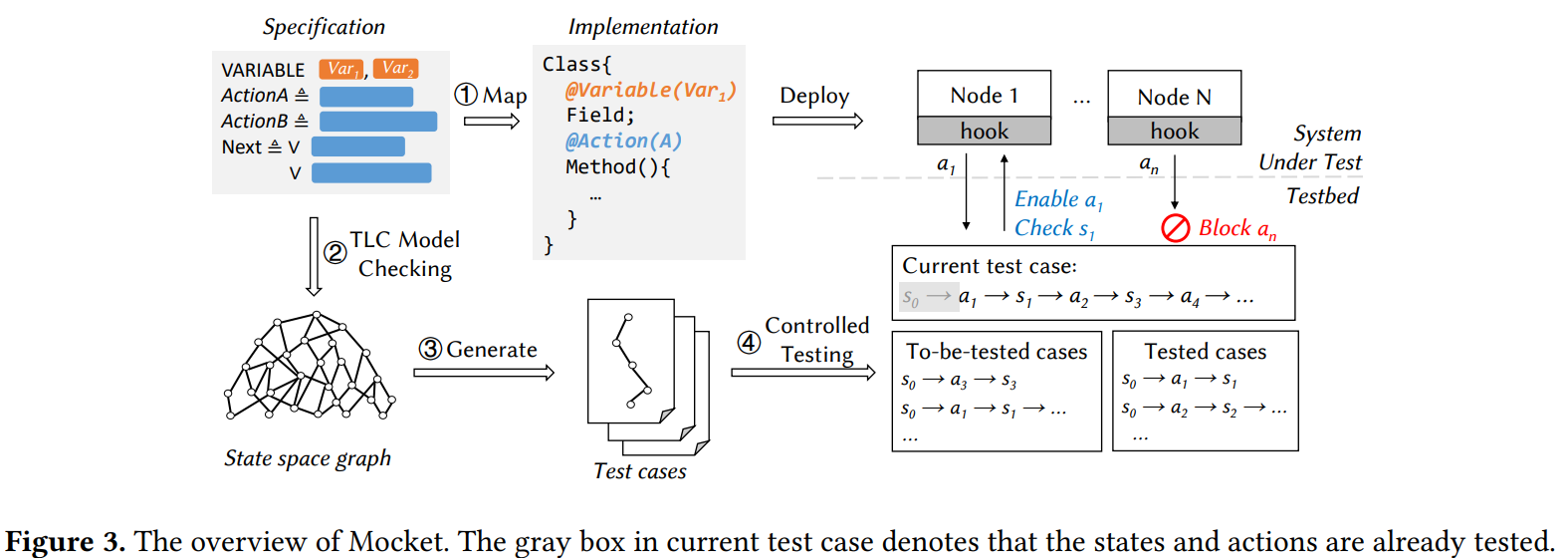
For the 150th reading group paper, we read “Model Checking Guided Testing for Distributed Systems” EuroSys’23 paper by Dong Wang, Wensheng Dou, Yu Gao, Chenao Wu, Jun Wei, and Tao Huang. We had a nice presentation of the paper, and I will be extremely short in my summary. The authors present and evaluate Mocket, a…
-
Reading Group #149. On-demand Container Loading in AWS Lambda
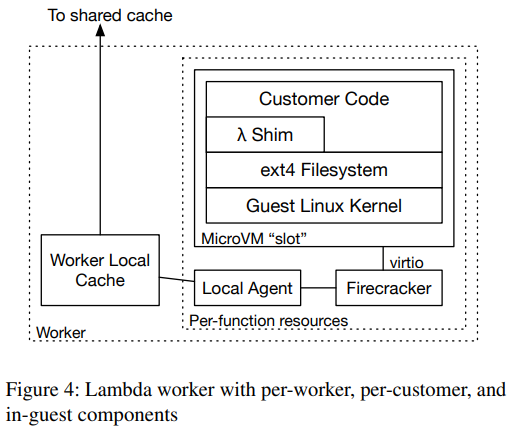
For the 149th paper in the reading group, we read “On-demand Container Loading in AWS Lambda” by Marc Brooker, Mike Danilov, Chris Greenwood, and Phil Piwonka. This paper describes the process of managing the deployment of containers in AWS Lambda. See, when AWS Lambda first came out, its runtime was somewhat limited — users could…
-
Winter 2023-2024 Reading Group Papers
Below is the reading group schedule for the upcoming winter term. The schedule is also available in our Google Calendar. Are you interested in joining the reading group? It is simple, join our Slack (which currently has ~1,500 members!) to get all the reading group updates and invites.
-
Reading Group. Oakestra: A Lightweight Hierarchical Orchestration Framework for Edge Computing
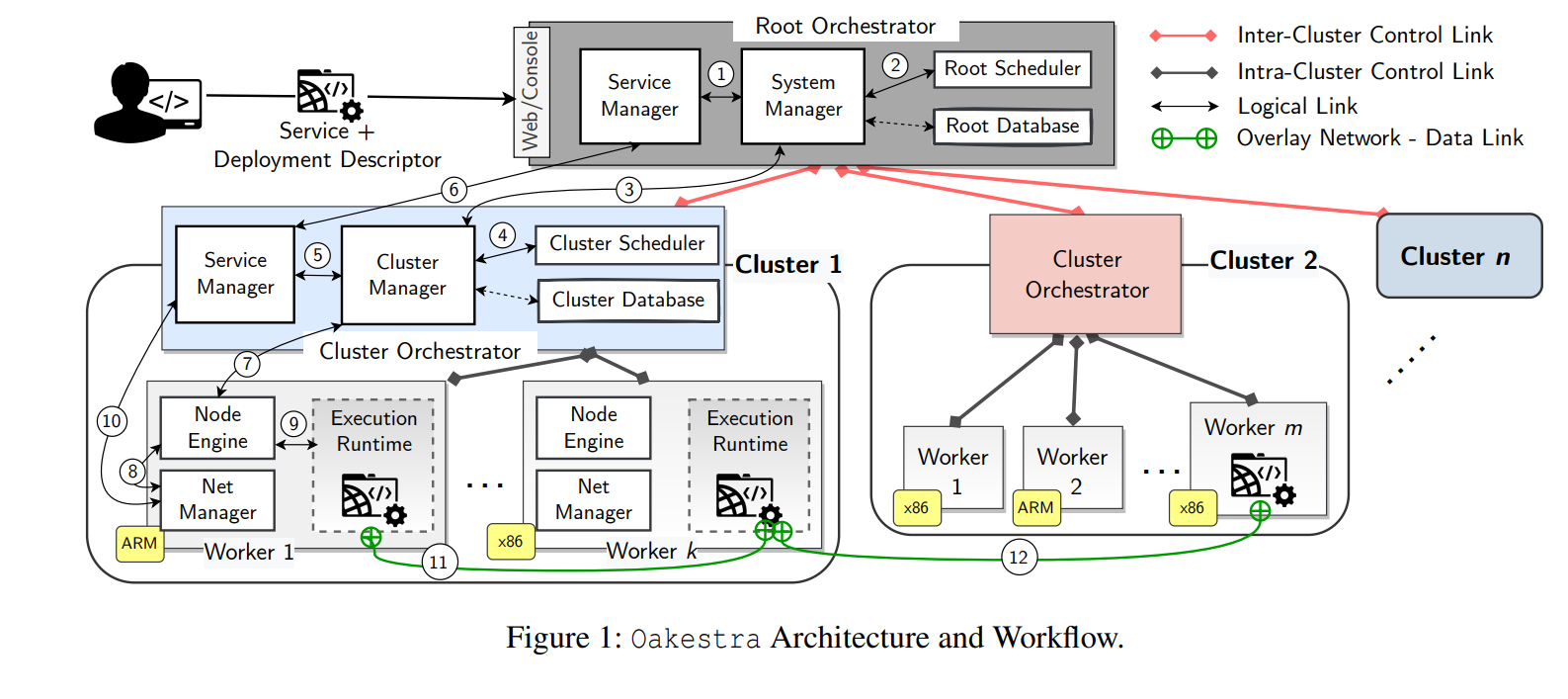
Our 148th paper in DistSys Reading Group was “Oakestra: A Lightweight Hierarchical Orchestration Framework for Edge Computing” by Giovanni Bartolomeo, Mehdi Yosofie, Simon Bäurle, Oliver Haluszczynski, Nitinder Mohan, and Jörg Ott. We had a very detailed presentation in the reading group, so I will make a very short summary to compensate. Oakestra, in a nutshell,…
-
Reading Group. Palette Load Balancing: Locality Hints for Serverless Functions
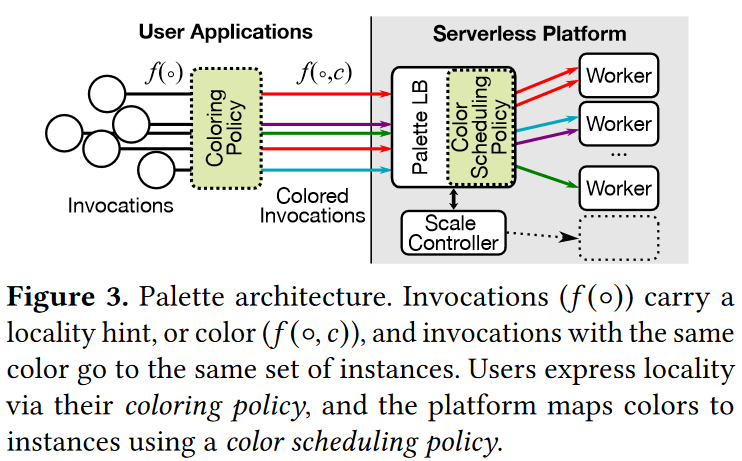
This week, our reading group focused on serverless computing. In particular, we looked at the “Palette Load Balancing: Locality Hints for Serverless Functions” EuroSys’23 paper by Mania Abdi, Sam Ginzburg, Charles Lin, Jose M Faleiro, Íñigo Goiri, Gohar Irfan Chaudhry, Ricardo Bianchini, Daniel S. Berger, Rodrigo Fonseca. I did a short improvised presentation since the…
-
Reading Group. Chardonnay: Fast and General Datacenter Transactions for On-Disk Databases
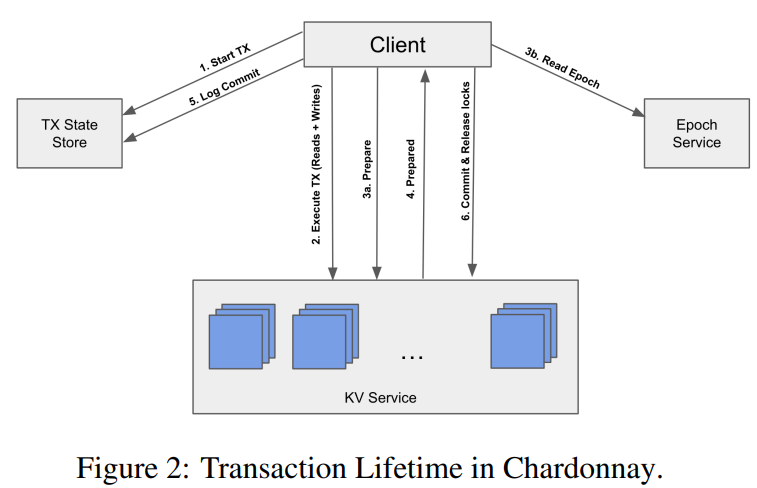
Last week, we looked at the “Chardonnay: Fast and General Datacenter Transactions for On-Disk Databases” OSDI’23 paper by Tamer Eldeeb, Xincheng Xie, Philip A. Bernstein, Asaf Cidon, Junfeng Yang. The paper presents a transactional database built on the assumption of having a very fast two-phase commit protocol. Coordination, like a two-phase commit (2PC), usually has…
I am an assistant professor of computer science at the University of New Hampshire. My research interests lie in distributed systems, distributed consensus, fault tolerance, reliability, and scalability.
@AlekseyCharapko
aleksey.charapko@unh.edu