We kicked off a new set of papers in the reading group with some fundamental reading – “Conflict-free Replicated Data Types.” Although not very old (and not the first one to suggest something similar to CRDTs), the paper we discussed presents a proper definition of Conflict-free Replicated Data Types (CRDTs) and the consistency framework around them. Needless to say, lots of research followed after this paper in the area of CRDTs.
It is impossible to discuss Conflict-free Replicated Data Types without mentioning the consistency in distributed replicated systems a bit. In super high-level terms, consistency describes how well a replicated system mimics a single copy illusion of data. On one side of the consistency spectrum, we have strong consistency (i.e. linearizability), that appears to an outside observer as if there is exactly one copy of the data. On the other side of the spectrum, we have eventual consistency, which allows many kinds of data artifacts, such as reading uncommitted data, accessing stale data, and more.
Strong consistency, however, comes at a significant performance cost that eventual systems do not have. For strong consistency, the order of operations is crucial, as clients must observe a single history of state changes in the system. Most often this means that all replicas must apply the same sequence of commands in the same order to progress through the same states of their state machines. This requires a sequencer node which often is a bottleneck. There are a few exceptions to this, for example, protocols like ABD do not need to have a single sequencer, and there may be even gaps/variations in history on individual nodes, but these protocols have other severe limitations. In addition to following the same history of operation, linearizability also imposes strict recency requirements — clients must observe the most recent state of the system. This prescribes synchronous replication to make sure enough nodes progress in lock-step for fault tolerance reasons. These challenges limit scalability — despite having multiple replicas, a replicated linearizable system will be slower than a single server it tries to mimic.
Eventually-consistent systems do not have such strong performance constraints, because there is no need to order operations, enforce recency, and even keep a single history of updates. This gives a lot of freedom to explore parallelism and push the boundaries of performance. Unfortunately, these systems are hard to program against, since the application built on top of an eventual consistency store needs to account/anticipate all kinds of data artifacts and deal with them.
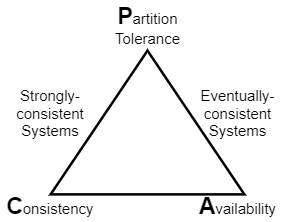
All these differences between strong and eventual consistency also mean that they land on different sides (vertices?) of the CAP triangle. With the recency requirements and lock-step execution, linearizable systems are CP, meaning that they sacrifice the Availability in the face of network Partitions and remain Consistent. Eventual systems… well, they do not promise Consistency at all, so they remain Available.
Anyway, the drastic differences between the two extremes of the consistency spectrum coupled with the scary CAP theorem have sparked a lot of research in consistency models that lie between strong and eventual. These intermediate models were supposed to provide a compromise between the safety of strongly consistent systems and the performance/availability of eventual ones. This is where CRDTs come to play, as they often drive the Strong Eventual Consistency (SEC) model. The paper presents SEC as the “solution to CAP”, and this makes me cringe a bit. First of all, Strong Eventual Consistency is a strongly confusing name. Secondly, having a solution to CAP sounds super definitive, whereas SEC is merely one of many compromises developed over the years.
Now we are getting to the meat of the paper that excites me. See, aside from a cringy name and a claim to solve CAP problems, SEC is pretty clever. A big problem with eventual consistency is that it does not define any convergence rules. Without such rules, the system may converge to an arbitrary state. Moreover, the convergence itself becomes unpredictable and impossible to reason about. SEC addresses the convergence problem by imposing some rules to the eventual consistency model. This enables engineers to reason about both the intermediate and final states of the system.
More specifically, SEC calls that any two identical nodes applying the same set of operations will arrive at identical states. Recall, that this sounds similar to how strongly consistent systems apply operations at nodes. The difference is that in strongly consistent systems we reason about sequences that have some order to them. In SEC, we work with sets of commands, which are order-less. I think this is a pretty cool thing, to throw away the order, yet still, ensure that the convergence is predictable and dependable on operations we have.
Completely throwing away the operation ordering and working with operation sets instead of sequences is tricky though. Consider some variable x, initially at x:=2. If we have two operations: (1) x:=x+2 and (2) x:=x*2, we can clearly see the difference if these operations are applied in a different order — by doing the operation (2) first, we will get a final state of 6 instead of 8. This presents a convergence problem and a violation of SEC if different nodes apply these operations in a different order. In a sense, these two operations, if issued concurrently, conflict with each other and require ordering. So clearly we need to be smart to avoid such conflicts and make SEC work.
There is no generic solution to avoid such conflicts, but we can design specific data structures, known as Conflict-free Replicated Data Types or CRDTs solve this ordering problem for some use cases. As the name suggests, CRDTs are built to avoid the conflicts between different updates or different versions of the same data object. In a sense, CRDTs provide a data structure for a specific use case with some defined and restricted set of operations. For instance, we can have a CRDT to implement a distributed counter that can only increment the counter’s value or a CRDT for an add-only set. The paper presents two broad types of CRDTs — state-based and operation-based CRDTs. Both types are meant for replicated systems and differ in terms of communicating the updates between nodes and reconstructing the final state.
State-based CRDTs transfer the entire state of the object between nodes, so they can be a bit heavier on bandwidth usage. The actual state of a data structure is not directly visible/accessible to the user, as this state may be different than the logical meaning of the data structure. For example, going back to the counter CRDT, logically we have a single counter, but we may need to represent its value as consisting of multiple components in order to ensure conflict-free operation. Assume we have n nodes, and so to design a state-based counter CRDT we break down the counter value to n registers <c1, c2, c3,…, cn>, each representing the increments recorded at a particular node. The logical state of CRDT counter is the sum of all registers \(c=\sum_{i=1}^nc_i\), which must be exposed through a query function. In addition to the query function, there must be an update function to properly change the underlying state. For the counter, the update function will increment the register corresponding to its node id.
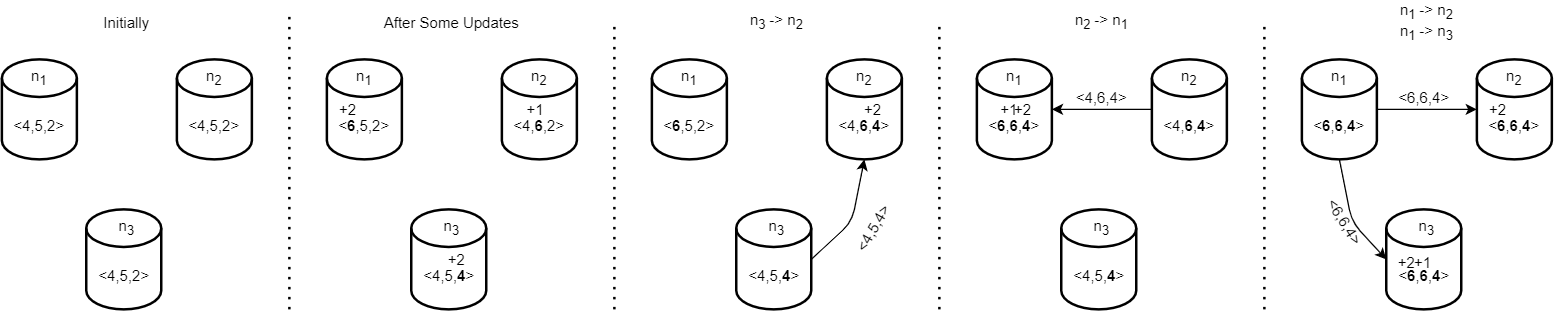
The most important part, however, is still missing. If some node receives concurrent increments, how can it reconcile them? Let’s say we have 3 nodes {n1, n2, n3}, each starting in some initial counter state <4,5,2>. These nodes receive some updates and increment their respective registers locally: n1:<6,5,2>, n2:<4,6,2>, n3:<4,5,4>. The nodes then send out their now divergent copies of the counter CRDT to each other. Let’s say node n2 received an update from n3, and now it needs to merge two versions of CRDT together. It does so with the help of the merge function, which merges the two copies and essentially enforces the convergence rules of SEC. There are some specific requirements regarding the merge function, but they essentially boil down to making sure that the order in which any two CRDTs merge does not matter at all. In the case of our counter, the merge function can be as simple as a pairwise comparison of registers between two versions of CRDT and picking the maximum value for each register. So for merge(n2:<4,6,2>, n3:<4,5,4>), we will see the updated value of <4,6,4> on node n2. If at this point n2 sends its update to n1, then n1 will have to do merge(n1:<6,5,2>,n2:<4,6,4>), and get the final version of <6,6,4>. Note that if n1 now also receives n3‘s update, it will not change the state of n1, since that update was already learned indirectly. This scheme works pretty neatly. It tolerates duplicate messages and receiving stale updates. However, we can also see some problems — we carry a lot more state than just a simple integer to represent the counter, and our counter’s merge function has restricted the counter to only allow increments. If we try to decrement a value at some node, it will be ignored, since the merge function selects the max value of a register. The latter problem can be fixed, but this will require essentially doubling the number of registers we keep for each node, exacerbating the state-size problem.
Operation-based CRDTs somewhat solve the above problems. Instead of transferring the full state of the object, op-based CRDTs move around the operations required to transform from one state to the next. This can be very economical, as operations may use significantly less bandwidth or space than the full CRDT state. For instance, in our counter CRDT example, the operation may be the addition of a number to the counter. Of course, as the operation may propagate at different speeds, and potentially get reordered, op-based CRDT requires that all concurrent operations are commutative. In other words, we again set the rules to ensure that the order of updates (i.e. operations) does not matter. In the counter use-case, we know that all additions commute, making it easy to implement an op-based counter. Unlike the state-based version, we do not even need to have multiple registers and sum them up to get the actual value of the counter. However, there are some important caveats with op-based CRDTs. They are susceptible to problems when a message or operation gets duplicated or resent multiple times. This creates a significant challenge, as either the operations themselves must be designed to be idempotent, or the operation delivery layer (communication component of the application) must be able to detect duplicates and remove them, essentially ensuring idempotence as well.
The paper goes into more details and more examples of each type of CRDT, as well as explaining how the two types are roughly equivalent in terms of their expressivity. Intuitively, one can think of the merge function as calculating a diff between two CRDT versions and applying it to one of the versions. Operations are like these diffs to start with, so it makes sense how the two types can be brought together. We have our presentation of the paper available here:
Discussion
1) Challenges designing CRDTs. As mentioned in the summary, CRDTs are special-purpose data structures, so designing them to fit a use case takes some time. I have spent some time a few years ago working on CRDTs at Cosmos DB, and it was a very fun thing to do, but also a bit challenging. A good example of the problem is a set CRDT. It is easy to make an add-only set, where items can be added and not removed. All set additions commute, so the problem is trivial. But to make sets more practically, we want to remove items too. A simple solution is to internally implement a removed set, so CRDT tracks all items added and removed separately. This way we can hardcode the precedence of adds and removes and say removes always come after ads for an item. But this works only as long as we do not ever need to re-add items back into the set…
2) Modeling. Due to their concurrency nature, it is a good idea to model and model-check CRDTs. I used TLA+ for this purpose. During the discussion, a question was raised on the best tools for CRDT model-checking, but unfortunately, nobody knew anything better than TLA+/TLC. I’d suspect that other tools used for verifying distributed systems, such as Alloy, could work as well.
3) Applications. Quite a bit of discussion was focused on applications that use CRDTs. we talked quite a bit about near-real-time collaborative tools, such as collaborative document editing. I mentioned the Google Docs style of application quite a few times, but it was brought up that Google actually uses Operational Transformation (OT) instead of CRDT. In particular, server-based OT, which requires a server to sync each client against. Regardless, collaborative tools seem to be the prime field for CRDTs. For instance, the Automerge library provides a good start for JSON-like CRDT to serve as the basis for these types of applications.